Summation of solutions to ODEs.
An ordinary differential equation (ODE) is an equation that contains one or several derivatives of an unknown function.
ADVANCED ENGINEERING MATHEMATICS - ERWIN KREYSZIG
- The ORDER of an ODE is defined as the degree of the highest derivative in the equation.
- An ODE is LINEAR if the dependent variable and its derivatives do not appear in products with themselves, raised to powers or in nonlinear functions. e.g. $\dot{y}+5y=cos(x)\rightarrow \text{$1^{st}$ order, linear}$ but $\dot{y}+5y=cos(y)\rightarrow \text{$1^{st}$ order, nonlinear}$.
- Put the dependent variable and its derivatives on the left-hand side of the equation.
- RHS=0: Homogeneous ODEs.
Principles to solve ODEs
- Direct inspection
- Separation of variable
- Integrating factors
Direct inspection
Exponential, e.g. $$ \frac{dx}{dt}=-4x\Rightarrow x(t)=Ce^{-4t} $$
Sinusoidal, e.g. $$ \ddot{x}+\lambda^2x=0\Rightarrow x(t)=sin(\lambda t)\text{ or }cos(\lambda t) $$
Separable ODEs
Given an ODE: $$ \frac{dx}{dt}=f(x,t) $$ Rearrange the equation: $$ g(x)\frac{dx}{dt}=h(t) $$ And then do integration: $$ \int g(x)dx=\int h(t)dt+C $$
Extended method: reduction to separable form
Make form below, and $\dot{x}\gets u$ $$ \dot{x}=f(\frac{x}{t}) $$
Exact ODEs
Exact case
The ODE's differential form $M(x,t)dx+N(x,t)dt$ is termed EXACT. Say
$$
M(x,t)\frac{dx}{dt}+N(x,t)=0\\
\frac{\partial u(x,t)}{\partial x}\frac{dx}{dt}+\frac{\partial u(x,t)}{\partial t}=0\\
\frac{\partial u(x,t)}{\partial x}dx+\frac{\partial u(x,t)}{\partial t}dt=0\\
\frac{du}{dt}=0\\
u=C
$$
(☞゚ヮ゚)☞ $u(x,t)$ or the exactness exists if:
$$
\frac{\partial M}{\partial t}=\frac{\partial N}{\partial x}
$$
Non-exact case
IF available
Say a non-exact equation:
$$
P(x,y)dx+Q(x,y)dy=0
$$
Use an integrating factor to make the equation exact:
$$
FPdx+FQdy=0
$$
Find the integrating factor: EXACTNESS
$$
\frac{\partial }{\partial y}(FP)=\frac{\partial }{\partial x}(FQ)\\
F_yP+FP_y=F_xQ+FQ_x\\
\text{Assume the simple cases where F depends on only x (or y)}\\
F=F(x)(\text{ or }F(y))\\
FP_y=F'Q+FQ_x\\
\frac{1}{F}\frac{dF}{dx}=\underset{R}{\frac{1}{Q}(P_y-Q_x)}\\
\text{Assume the simple case where R depends only on x}\\
F(x)=exp\int R(x)dx
$$
IF unavailable
Choose other methods.
Solutions to specific forms of ODEs
1st-order ODEs
Linear cases
$$ \dot{x}+p(t)x=r(t) $$
Homogeneous case: $\dot{x}+p(t)=0$ $$ x(t)=A\cdot exp\left(-\int p(t)dt\right) $$
Non-homogeneous case: $\dot{x}+p(t)x=r(t)$. Apply integrating factor: $$ F=exp\left(\int p(t)dt \right) $$
$$ x(t)=e^{-\int p(t)dt}\left[\int e^{\int p(t)dt}r(t)dt+C \right] $$
Proof:

Non-linear cases: Bernoulli equation
$$ \dot{y}+p(x)y=g(x)y^a $$
Let $u(x)=y^{1-a}$, then $$ \dot{u}+(1-a)pu=(1-a)g $$
2nd-order linear ODEs
$$ \ddot{y}+p(x)\dot{y}+q(x)y=r(x) $$
Homogeneous cases
Linear cases with coefficients as functions
Homogeneous case: $\ddot{y}+p(x)\dot{y}+q(x)y=0$. Superposition principle: any linear combination of two solutions on an open interval is again a solution.
Reduction of order. (when one solution $y_1$ is known). Set $y_2=uy_1$. $$ y_2=y_1u=y_1\int \frac{1}{y_1^2}e^{-\int pdx}dx $$
Linear cases with constant coefficients
Homogeneous ODE: $$ \ddot{y}+a\dot{y}+by=0 $$ Characteristic equation (derived from putting $y=e^{\lambda x}$ into the equation): $$ \lambda^2+a\lambda+b=0\Rightarrow\lambda_1,\lambda_2 $$ Solutions: $y_1=e^{\lambda_1 x}$ and $y_2=e^{\lambda_2 x}$ .
Two distinct real roots
Solution: $$ y=c_1e^{\lambda_1x}+c_2e^{\lambda_2x} $$
Real double root
$$ \lambda=\lambda_1=\lambda_2=-\frac{a}{2} $$
Known $y_1=e^{-(a/2)x}$. Apply Reduction of Order: $y_2=uy_1$, then, $$ u=c_1x+c_2\Rightarrow u=x\text{ , simple case} $$ Solution: $$ y=(c_1+c_2x)e^{-ax/2} $$
Complex roots
$$
\begin{aligned}
\lambda_1&=-\frac{1}{2}a+i\omega\
\lambda_2&=-\frac{1}{2}a-i\omega
\end{aligned}
$$
$$
\begin{aligned}
y_1&=e^{-\frac{1}{2}a+i\omega}=e^{-ax/2}cos\omega x\
y_2&=e^{-\frac{1}{2}a-i\omega}=e^{-ax/2}sin\omega x
\end{aligned}
$$
Solution: $$ y=e^{-ax/2}(Acos\omega x+Bsin\omega x) $$ Properties:
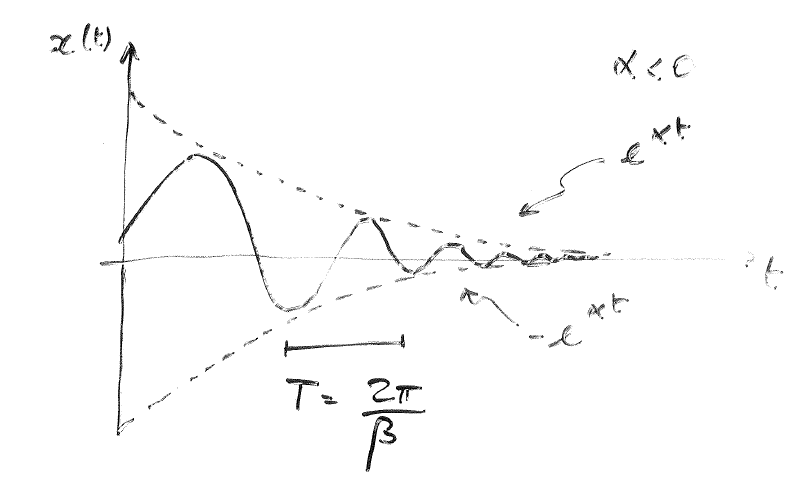
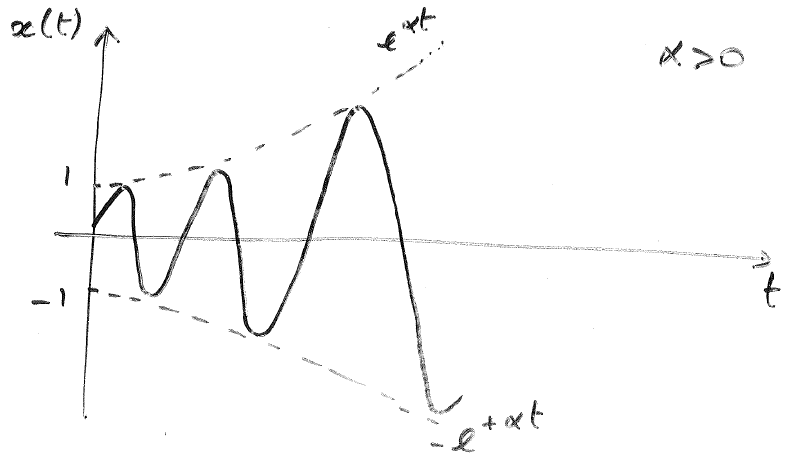
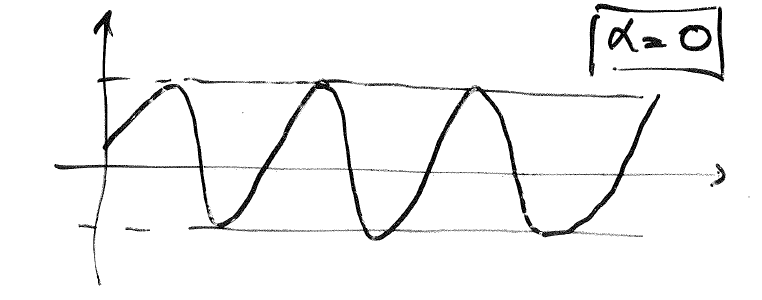
Summary in table:

Non-homogeneous cases
$r(x)\neq 0$. Superposition principle may not exist. $$ \ddot{y}+p(x)\dot{y}+q(x)y=r(x) $$ GENERAL SOLUTION: homogeneous solution + particular solution $$ y(x)=y_h(x)+y_p(x) $$ Find the PARTICULAR SOLUTION: Method of undetermined coefficients.
Constant coefficients $$ \ddot{y}+a\dot{y}+by=r(x) $$ Choose a form for $y_p$ similar to $r(x)$, but with unknown coefficients to be determined by substituting that $y_p$ and tis derivatives into the ODEs. More rules:

